리뷰 Intro
테스트 셋에 대해 강화학습을 적용했을 때 (label이 없다는 가정) 충분한 성능 향상을 볼 수 있다는 논문이다. label이 없을 때를 가정해 majority voting으로 pseudo-label을 만들고 그걸 바탕으로 RL을 적용한다. 충분히 해 볼 수 있는 생각이기에 방법 자체는 매우 단순하다. 다만, 의외로 성능 향상이 크고 그에 대한 다양한 결과 분석을 담고 있으며 통찰이 돋보이는 분석도 있다. 특히 pseudo-label이 틀렸더라도 어차피 많은 답변들 중 하나이기때문에 나머지 답변들에 대해 틀렸다고 reward를 주고 학습을 하는 것이 모델을 평균적으로 옳은 방향으로 학습되게 만들어 충분히 학습이 가능하다는 분석이 흥미롭다.
테스트 셋으로만 학습되었다보니 아직 대규모 데이터셋에 대해 검증되지 않았다. 하지만 앞으로의 방향은 label이 없는 대규모 데이터셋에 대한 selfsupervised learning쪽이 될 것이기 때문에 충분히 다양한 후속 연구가 나올 것으로 기대된다.
결론: 중요도 (4/5)
github: https://github.com/PRIME-RL/TTRL
GitHub - PRIME-RL/TTRL: TTRL: Test-Time Reinforcement Learning
TTRL: Test-Time Reinforcement Learning. Contribute to PRIME-RL/TTRL development by creating an account on GitHub.
github.com
Abstract
- 이 논문은 LLM의 추론 과제에서 명시적인 정답 레이블이 없는 데이터에 대해 RL (강화학습)을 적용하는 방법을 탐구함.
- 이 문제의 핵심 도전 과제는 정답 정보를 알 수 없는 상태에서 추론 시 보상을 어떻게 추정하느냐에 있음. 겉보기에는 어려워 보이지만, 우리는 Test-Time Scaling(TTS)에서 일반적으로 사용되는 방식인 다수결 투표(majority voting)와 같은 기법이 RL 훈련에 적합한 효과적인 보상을 제공할 수 있음을 발견.
- 본 연구에서는 레이블 없는 데이터를 사용해 RL로 LLM을 훈련시키는 새로운 방법인 Test-Time Reinforcement Learning(TTRL)을 제안함. TTRL은 사전 학습된 모델의 사전 지식(prior)을 활용해 LLM이 스스로 진화하도록 함.
- 실험 결과, TTRL은 다양한 과제와 모델에서 일관된 성능 향상을 보임. 특히 TTRL은 정답 레이블이 없는 테스트 데이터만을 사용했음에도, Qwen-2.5-Math-7B의 AIME 2024 기준 pass@1 성능을 약 159% 향상시킴.
- 또한 TTRL은 Maj@N이라는 단일 평가 지표에 의해서만 감독을 받음에도 불구하고, 초기 모델의 성능 한계를 꾸준히 초과하고, 정답 레이블로 직접 훈련된 모델에 근접하는 성능을 보여줌. 이러한 실험 결과는 TTRL이 다양한 과제에 대해 일반적으로 효과적임을 입증하며, 보다 폭넓은 작업 및 도메인으로의 확장 가능성을 시사함.

1 Introduction
- Test-Time Scaling(TTS)은 대형 언어 모델(LLM)의 추론 능력을 향상시키기 위한 새로운 접근 방식으로 주목받고 있음. 최근 연구들은 TTS가 사전 학습(pre-training) 중 스케일링보다 계산 효율이 더 뛰어나며, 동일한 연산 자원으로 더 우수한 성능을 달성할 수 있음을 시사함. 많은 연구들이 보상 모델을 활용하거나 디코딩 과정에서 다수결 투표 및 몬테카를로 트리 탐색(MCTS)과 같은 전략을 통해 TTS를 향상시키려 시도해옴.
- TTS: 성능을 테스트 시점에 향상시키는 방법론
- 테스트 시점에 학습시키는게 아니라 확률분포상의 다양성으로부터 좋은 선택지를 이끌어내는 식. 대표적으로 아래 방법들 포함:
- Majority Voting (다수결 투표)
여러 번 응답을 생성한 후 가장 자주 나오는 답을 정답으로 간주합니다. 예: 하나의 질문에 대해 모델이 5번 답변하고, 그 중 가장 많이 나온 답을 선택. - Temperature Scaling
디코딩 단계에서 softmax의 temperature를 조절하여 샘플링 분포를 조정해 더 다양하거나 더 결정적인 출력을 유도. - Self-Consistency Decoding
CoT(Chain-of-Thought)를 활용해 여러 개의 추론 경로를 생성하고, 그 결과를 종합해 일관된 답을 추론. - Monte Carlo Tree Search (MCTS)
탐색 기반 기법을 디코딩 과정에 적용하여 더 나은 답을 찾음.
MCTS의 경우 기본적으로는 답을 알아야 정답과 비교해 해당 트리의 가중치를 올릴 수 있기 때문에 정답을 알아햐 하지만, majority voting과 같은 방법을 통해 정답 없이도 트리의 가중치를 업데이트하는 방식을 적용하는 듯 함.
- Majority Voting (다수결 투표)
- 테스트 시점에 학습시키는게 아니라 확률분포상의 다양성으로부터 좋은 선택지를 이끌어내는 식. 대표적으로 아래 방법들 포함:
- TTS: 성능을 테스트 시점에 향상시키는 방법론
- 최근의 대표적인 LRM (대형 추론 모델)들인 DeepSeek-R1과 OpenAI의 o1은 RL이 장기적인 chain-of-thought 추론을 향상시키는 데 중요한 역할을 한다는 점을 강조하고 있음. 그러나 이러한 LRM들은 여전히 라벨이 없는 새로운 데이터 스트림을 처리하는 데에는 한계를 보이고 있음. 예를 들어, OpenAI o3는 ARC-AGI-1에서는 75.7%의 성공률을 보이지만, ARC-AGI-2(2025)에서는 문제의 4%만을 해결.
- 이러한 TTS 관련 연구들은 훈련 시기(train-time)와 테스트 시기(test-time)의 모델 동작 사이에 분명한 차이가 존재함을 보여주며, 특히 RL 기반 접근 방식에서 이러한 경향이 두드러짐.
- 그러나 RL을 대규모 훈련 데이터에만 적용하는 것은 새롭게 등장하는 복잡한 입력이나 분포 변화에 대응하기에 매우 불충분함. 최근에는 테스트 시점에서 입력된 데이터를 이용해 모델의 매개변수를 업데이트할 수 있는 Test-Time Training(TTT) 기법이 주목받고 있음. 이러한 기법들은 RL을 활용한 테스트 시 fine-tuning을 가능하게 하며, TTS의 일반화 성능을 향상시킬 수 있는 자연스럽고 유망한 방향으로 여겨짐. (적절한 답을 정답으로 간주해 업데이트 하는 방식이 아닐지)
- 하지만 여기에는 중요한 문제점이 하나 존재. 바로 테스트 시점에서 어떻게 RL의 보상 또는 검증자를 얻을 수 있는가 하는 것. 현실 세계의 과제가 점점 더 복잡해지고 다양해짐에 따라, 이러한 데이터를 대규모로 수작업으로 주석 처리하여 RL을 학습시키는 것은 점점 더 비현실적이 되고 있음. 이 문제는 선도적인 모델들의 지속적인 학습을 가로막는 주요 장벽이 됨.
- 이러한 문제를 해결하기 위해 우리는 Test-Time Reinforcement Learning(TTRL)을 제안한다. TTRL은 테스트 시점에서 RL을 통해 모델을 학습시키는 방법. TTRL은 반복 샘플링 전략을 사용하여 라벨을 추정하고, 규칙 기반 보상을 계산함으로써 라벨이 없는 데이터에서도 RL을 가능하게 함. 효과적인 majority voting reward을 활용함으로써, TTRL은 정답이 없는 상황에서도 효율적이고 안정적인 RL 학습을 가능하게 함.
- 앞서 언급했듯이, 더욱 복잡한 과제가 증가함에 따라 라벨이 없는 데이터의 비율도 필연적으로 증가할 것. TTRL은 명시적인 감독 없이 모델을 학습시키는 문제를 직접적으로 다루며, 이러한 어려운 환경 속에서 모델이 스스로 탐색하고 학습할 수 있는 능력을 평가함. 본질적으로 TTRL은 모델이 스스로 경험을 생성하고, 보상을 추정하며, 시간이 지남에 따라 성능을 향상시키도록 만듦.
- 실험 결과, TTRL을 Qwen2.5-Math-7B에 적용했을 때 AIME 2024에서 성능이 13.3에서 43.3으로 159% 향상되었으며, AMC, AIME, MATH-500을 포함한 평균 성능은 84% 향상됨. 이 모든 성과는 라벨이 없는 테스트 데이터만을 사용한 자기 진화를 통해 달성되었으며, 다른 과제에도 일반화되는 성과를 보임. TTRL은 pass@1 성능을 향상시킬 뿐만 아니라, 다수결을 통한 TTS 향상에도 기여. 또한 초기 실험에 따르면, TTRL은 다양한 크기와 유형의 모델에서도 효과적이며 기존 RL 알고리즘과도 통합이 가능함. 우리는 TTRL이 높은 성능 상한을 갖는다는 긍정적인 특성도 관찰함. 이러한 결과는 TTRL이 인간의 주석 작업에 대한 의존도를 크게 줄이고, RL을 대규모 비감독 학습으로 확장시킬 수 있는 가능성을 보여줌.
2 Test Time Reinforcement Learning (TTRL)
- 정답 라벨 없이 사전 학습된 모델을 테스트 시점에 강화학습을 통해 학습시키는 문제를 연구
2.1 Methodology

- Fig. 2는 TTRL이 이 문제를 어떻게 해결하는지를 보여줌. 프롬프트 $x$로 표현되는 상태가 주어졌을 때, 모델은 정책 $\pi_\theta(y\mid x)$에 따라 출력 $y$를 생성함으로써 행동한다. 이 정책은 파라미터 $\theta$에 의해 정의됨.
- 정답 label 없이 보상 신호를 구성하기 위해, 모델로부터 여러 후보 출력 $\{y_1,y_2,\dots, y_N\}$을 반복 샘플링을 통해 생성. 그 후 다수결 투표나 다른 집계 방식을 통해 합의된 출력 $y^*$를 도출하고, 이를 최적 행동의 대리(proxy)로 사용 (정답으로 간주).
- 환경은 샘플링된 행동 $y$와 합의된 행동 $y^*$사이의 일치 정도에 따라 보상 $r(y, y^*)$을 제공. 따라서 강화학습의 목표는 아래 정의된 기대 보상을 최대화하는 것:$$\max_{\theta} \mathbb{E}_{y \sim \pi_{\theta}(\cdot \mid x)} \left[ r(y, y^*) \right]$$
- 파라미터 $\theta$는 그래디언트 상승법(gradient ascent)을 통해 업데이트됨:$$\theta \leftarrow \theta + \eta \nabla_{\theta} \mathbb{E}_{y \sim \pi_{\theta}(\cdot \mid x)} \left[ r(y, y^*) \right]$$
- 여기서 $\nabla\는 learning rate.
- 이 접근 방식은 모델이 추론 과정에서 적응할 수 있게 하며, 라벨이 없는 데이터에서도 분포가 변화된 입력에 대해 성능을 효과적으로 향상시킬 수 있도록 함.
2.2 Majority Voting Reward Function
- majority voting reward은 먼저 다수결 투표를 통해 label을 추정한 후, 이 추정된 label을 기반으로 규칙 기반 보상을 계산하여 최종 보상으로 사용하는 방식. 주어진 질문 $에 대해, 먼저 $를 LLM에 입력하여 출력 집합을 생성. 그런 다음, 정답 추출기가 이 출력들을 처리하여 예측된 답변들의 집합 $P = \{\hat{y}_i\}_{i=1}^{N}$을 얻음. 이후 $P$에 대해 식 4를 따라 다수결 투표를 점수 함수 $s(y, x)$로 사용하여 가장 자주 등장한 예측 $를 얻고, 이를 추정된 라벨로 간주함. 이 다수결로 결정된 예측 $y$는 그 다음 단계에서 규칙 기반 보상을 계산하는 데 사용. 보상은 1 또는 0의 binary로 주어짐.

3 Experiments
3.1 Experimental Setup
모델:
- TTRL의 범용성을 다양한 백본 모델에 걸쳐 평가하기 위해, 우리는 베이스 모델과 인스트럭트 모델 모두를 사용하여 실험을 수행함. TTRL이 효과적으로 확장 가능한지를 평가하기 위해, 베이스 모델로는 Qwen2.5-Math-1.5B와 Qwen2.5-Math-7B(Yang et al., 2024)를 실험에 사용함. Instruct 모델의 경우, 다양한 모델 계열에서 TTRL의 효과를 검증하기 위해 LLaMA-3.1-8B-Instruct(Grattafiori et al., 2024)를 사용함.
벤치마크:
- TTRL은 세 가지 수학 추론 벤치마크에서 평가함: AIME 2024(Li et al., 2024), AMC(Li et al., 2024), 그리고 MATH-500(Hendrycks et al., 2021). 각 벤치마크에 대해 TTRL을 개별적으로 적용한 후, 이전 연구와의 공정한 비교를 위해 greedy decoding 방식을 사용하여 pass@1을 측정함. 또한 DeepSeek-R1(Guo et al., 2025)의 디코딩 파라미터를 사용하여 Figure 6에서 Avg@64 점수를 함께 보고함으로써 보다 신뢰도 있는 평가를 제공함.
비교 기준(Baseline):
- TTT(Test-Time Training)를 추론 성능 향상에 활용한 연구는 기존에 없었기 때문에, 우리는 주로 백본 모델 자체와 비교함으로써 TTRL이 자기 진화를 통해 성능 향상을 달성할 수 있는지를 검증함. 두 개의 베이스 모델에 대해서는, 대규모 후처리를 거친 인스트럭트 버전과의 비교도 함께 수행함. 또한 참고용으로, 유사한 백본을 사용하고 RL 기반으로 광범위하게 학습된 현재의 대표적인 “R1-Zero-Like” 모델들도 포함함: DeepSeek-R1-Distill-1.5B&7B, SimpleRL-Zero-7B, PRIME-Zero-7B, OpenReasonerZero-7B, Oat-Zero-1.5B&7B, LIMR. 단, TTRL은 기존 모델들과 설정이 다르기 때문에, 이 비교는 엄밀히 말해 공정하지 않을 수 있음.
구현 세부사항:
- 우리는 TTRL 구현을 위해 각 벤치마크에 대해 GRPO를 독립적으로 적용. 하이퍼파라미터로는, 학습률을 $5 \times 10^{-7}$로 고정하고, 정책 모델에 AdamW 옵티마이저를 적용. rollout 단계에서는 label 추정을 위해 temperature 1.0으로 64개의 응답(단, MATH-500에서는 32개)을 샘플링하고, 프롬프트당 16개의 응답을 다운샘플링하여 학습에 사용함. 우리의 vote-then-sample 전략은 계산 비용을 줄이면서도 높은 성능을 유지하는 데 효과적임을 입증. 생성 토큰 최대 수는 3072로 설정하였고, KL 계수는 모든 실험에서 0으로 설정하였음. 학습 에피소드 수는 데이터셋 크기 및 과제 난이도에 따라 각각 MATH에는 40, AMC에는 50, AIME에는 60으로 설정함.
3.2 Main Results

TTRL은 대부분의 과제와 모델에서 우수한 성능을 보임
- label 없는 테스트 데이터만을 이용한 자기 진화(self-evolution)에만 의존함에도 불구하고, TTRL은 대규모 레이블링 데이터셋으로 학습된 기존의 RL 기반 모델과 유사한 수준의 성능을 달성함 (Table 1)
- 매우 도전적인 수학 추론 벤치마크인 AIME 2024에서 TTRL은 무려 159.3%의 성능 향상을 이루며, 대규모 데이터셋으로 학습된 모든 기존 모델들을 능가함. 또한 Qwen2.5-Math-7B에 적용했을 때, 세 개의 벤치마크 전반에서 평균 84.1%의 성능 향상을 보임.
TTRL은 자연스럽게 스케일링됨
- 또 다른 중요한 관찰은 모델 크기가 증가할수록 (1.5B에서 7B로), AIME 2024와 AMC 모두에서 성능 향상이 더욱 커진다는 점임. 이는 TTRL이 지닌 자연스러운 스케일링 특성을 보여줌. 더 큰 모델은 자기 개선 과정에서 보다 정확한 다수결 보상을 생성할 수 있으며, 이로 인해 새로운 데이터에 대한 학습이 더욱 효과적으로 이루어짐.
- 반면, LLaMA-3.1-8B-Instruct와 Qwen2.5-Math-1.5B는 TTRL을 통해 AIME 2024에서 의미 있는 성능 향상을 이루지 못했는데, 이는 모델 용량의 한계 때문으로 보임. 그에 비해 Qwen2.5-Math-7B는 더 큰 모델 용량과 풍부한 지식을 기반으로 자기 개선을 통해 명확한 성능 향상을 얻을 수 있었음.
TTRL은 목표 과제를 넘어 일반화됨
- 우리는 각 벤치마크에 대해 TTRL을 수행한 후, 이를 다른 벤치마크에도 평가하여 일반화 능력을 테스트함 (Qwen2.5-Math-7B 사용, Fig. 3). 이 설정은 분포 밖(out-of-distribution)에 해당함에도 불구하고, TTRL은 모든 벤치마크에서 상당한 성능 향상을 이끌어냄. 이는 TTRL이 특정 과제에 과적합(overfitting)하여 다른 과제에서 성능을 희생하는 것이 아니라, 자기 개선을 통해 일반화 가능한 이득을 얻고 있음을 시사함.

TTRL은 다양한 RL 알고리즘과 호환됨
- 우리는 MATH-500에서 PPO를 사용하여 TTRL을 적용해, TTRL이 다양한 강화학습 알고리즘과 호환 가능한지를 평가함. 그 결과 PPO와 GRPO의 성능 추이는 유사하게 나타났으며, GRPO와 비교할 때 PPO는 더 안정적인 결과를 보이면서도 비슷한 수준의 전반적인 성능을 달성.
- 간단하게 차이를 보자면 PPO는 점수 평가자가 답변에 대한 점수를 측정해 이를 바탕으로 정책을 업데이트. GRPO는 답변들 사이의 랭킹을 매겨 랭킹이 높은 답변에 더 높은 점수를 주는 방향으로 정책을 업데이트

3.3 Training Dynamics
- Fig. 5는 Qwen2.5-Math-7B 모델을 AIME 2024에 적용한 예시로서 TTRL의 두 개의 학습 곡선을 보여줌.

4 Discussion
4.1 Q1: How Well Can TTRL Perform?
- TTRL은 초기 모델의 학습 신호와 직관적인 상한선인 Maj@N을 능가할 뿐만 아니라, 정답이 포함된 테스트 데이터를 사용하여 직접 강화학습한 경우의 성능에 근접함. 이러한 성능 향상은 TTRL이 테스트 시점 학습에 RL을 활용하는 방식 덕분일 수 있음. 즉, 다수결 기반의 pseudo-label을 보상으로 변환함으로써, 효과적인 감독 품질을 향상시키고, 동시에 학습을 Maj@N이 가진 구조적 한계로부터 분리.
- TTRL의 경험적 상한선은 테스트 데이터에 대한 학습(즉, 테스트 데이터를 그대로 학습에 사용하는 경우)이며, 이는 기존의 표준 학습-평가 방식보다 더 높은 효율성과 가능성을 시사함.
- 특히 어려운 과제에 대해서도, TTRL은 단지 15억 파라미터(1.5B)의 모델만으로도 경험적 상한선에 도달할 수 있음. 이는 대형 언어모델(LLM)이 이제 TTRL을 통해 효율적으로 자기 진화를 수행할 수 있으며, 대규모 데이터셋에 대한 "제한 없는 평생 학습(unbounded lifelong learning)"이 가능함을 보여줌.
- 우리는 TTRL의 잠재적인 성능을 두 가지 상한선을 기준으로 분석함. 첫 번째 상한선은 TTRL 학습 중 보상 계산에 사용되는 Maj@N이며, 두 번째 상한선은 정답 label에 접근할 수 있다고 가정하고 벤치마크 데이터셋을 직접 학습하는 경우로, 이는 label 정보가 정책 모델에 누출(leakage)되는 설정이다.
TTRL은 Maj@N에 의해 감독되지만, 이를 능가함
- TTRL은 모델이 스스로 생성한 다수결 기반 출력(majority-voted output)을 사용하여 강화학습을 수행하기 때문에, 해당 다수결 성능은 직관적으로 최종 성능의 상한선으로 간주될 수 있음. 그러나 놀랍게도 학습 후, 모델은 이 예상 상한선에 도달하는 것뿐만 아니라 이를 초과하였으며, 이는 곧 모델이 스스로 제공한 감독 신호를 넘어서 개선되었음을 의미함.
- Fig. 6은 Qwen2.5-Math-7B 모델에 대한 TTRL 결과를 보여. TTRL의 Avg@64는 모든 벤치마크에서 Qwen2.5-Math-7B의 Maj@64보다 높은 성능을 보여주었으며, 이는 예상을 크게 뛰어넘는 결과. 또한, TTRL의 성능은 Majority Voting을 적용했을 때 현저히 향상되었는데, 이는 언어 모델이 자신의 출력을 학습 재료로 삼아 훈련함으로써 성능을 개선할 수 있음을 시사함. 특히 주목할 점은, 자기 강화 루프(self-reinforcing loop)를 통해 모델이 스스로를 끌어올려 예상된 성능 상한선을 뛰어넘는 방향으로 진화한다는 것. (Maj@N: 다수결 답변이 실제 정답과 일치하는 비율. Avg@N: 평균적으로 답변들 중 정답의 비율. 결로적으로 majority voting에 기반하여 학습했음에도 실제 정답을 말하는 개수가 크게 늘어남. 맞춘 적 없는 문제를 맞추는 경우는 있었을지..?)

TTRL의 성능 향상은 벤치마크 학습 성능에 근접함
- TTRL의 동기는 다수결을 통해 pseudo-label을 추정하고, 이를 기반으로 보상을 계산하여 정답 라벨 없이도 효과적인 자기 개선을 가능하게 하는 데 있음. 따라서 TTRL의 자연스러운 상한선은 테스트 데이터를 직접 사용하여 RL을 수행하는 설정이며, 이를 RL (leakage)라고 표현함.
- 우리는 Qwen2.5-Math-7B를 사용하여 MATH-500에서 TTRL과 RL (leakage)를 각각 수행하고, 그 성능을 비교하였다 (Fig. 7). 놀랍게도, TTRL의 성능 곡선은 RL (leakage)의 성능에 매우 근접하는 것으로 나타남.
- 즉, TTRL은 정답 라벨이 없는 비감독 학습 환경에서도, 마치 감독 학습을 수행한 것과 비슷한 수준의 자기 개선 효과를 RL을 통해 달성할 수 있음. 이는 TTRL의 효율성과 성능 잠재력이 상당하다는 것을 보여줌.
- 또한, TTRL은 소형 LLM조차도 입력만 주어지는 어려운 과제에 대해 효과적으로 자기 개선이 가능하다는 증거를 제시함. Qwen2.5-Math-1.5B의 실험 결과도 이를 뒷받침하는데, 해당 모델은 MATH-500에서 초기 성능 33.0에서 출발해 TTRL을 통해 142.4% 향상된 80.0의 성능을 기록하며, 명확한 자기 개선을 입증함.

4.2 Q2: Why Does TTRL Work?
Label Estimations
- TTRL과 표준 강화학습 알고리즘의 직접적인 차이점 중 하나는, TTRL은 label을 추정해야 한다는 점이며, 이 과정은 보상의 부정확성을 유발할 수 있음. 그럼에도 불구하고 TTRL이 작동하는 이유는 다음 두 가지로 설명할 수 있음:
- 기존 연구들에 따르면, 강화학습은 어느 정도의 보상 오류를 허용할 수 있음. 특히 강화학습은 종종 학습 데이터를 암기하는 방식에 의존하는 SFT보다 일반화 성능이 더 뛰어난 경향이 있음. RL에서는 보상이 명확한 정답이기보다는 탐색을 위한 방향성 신호(directional signal) 역할을 하며, 이로 인해 보상 노이즈에 강인한 특성이 있음.
- 보상 모델의 최적화 관점에서, 정확한 보상 모델이 반드시 더 나은 교사(teacher)가 되는 것은 아니라는 연구 결과도 있음.
따라서, 정책 모델이 스스로 추정한 보상 신호가 오히려 학습에 더 적합한 안내 역할을 할 수 있음.
Reward Calculations
- 모델이 다수결 투표를 통해 정확한 라벨을 추정할 수 있는 경우, 그에 따라 계산된 보상도 일반적으로 신뢰할 수 있음.
하지만 자연스러운 의문이 발생: 모델이 AIME 2024와 같은 어려운 벤치마크에서 정확한 라벨을 추정하지 못하는 상황에서도 TTRL은 왜 여전히 효과적인가? - 가장 근본적인 이유는 강화학습에서의 보상 정의에 있음. 규칙 기반 보상은 예측된 답변이 "label"과 일치하는지 여부에 따라 부여됨. 즉, 추정된 라벨이 실제 정답이 아니더라도, 예측된 응답과 다르기만 하면 올바른 "negative reward"을 줄 수 있음.
사례 분석: AIME 2024에서의 TTRL

- Qwen2.5-Math-7B를 사용한 AIME 2024 벤치마크에서의 TTRL 성능을 통해, 보다 구체적인 사례를 살펴봄. Fig. 8은 세 가지 메트릭의 변화 곡선을 보여줌. 우리는 AIME 2024에서 TTRL이 효과적인 이유로 두 가지를 식별:
- 보상 신호는 label보다 더 밀도 있게분포되어 있어, 추정 label이 부정확하더라도 유용한 학습 신호를 회복할 수 있는 기회가 많음. 예를 들어, 추정된 label이 틀리더라도 같은 rollout 내의 다른 출력이 올바른 보상이나 고품질 보상을 만들어낼 수 있음. 이로 인해 전체적인 보상 신호는 pseudo-label의 오류에 대해 더 robust해짐.
- 또 하나의 흥미로운 현상은, 모델의 성능이 낮을수록 오히려 보상 추정이 더 정확해질 수 있다는 점. 베이스 모델의 경우, 가장 많이 예측된 답변의 비율은 전체 예측의 단 16.6%에 불과. 따라서 라벨이 정확히 추정되지 않더라도, 모델의 응답이 매우 다양하고 일관되게 부정확하기 때문에 대부분의 예측에 대해 정확한 보상을 부여할 수 있음. 이는 역설적으로 모델이 실수를 많이 할수록 보상 신호는 오히려 정확해지는 경향을 보임.

- 이러한 주장을 뒷받침하는 실증적 관찰은 Label Accuracy와 Reward Accuracy의 비교에서 확인할 수 있음 (Fig. 8). 대부분의 label accuracy는 20~50% 범위에서 변동하지만, reward accuracy는 초기부터 92%에 달하는 높은 수치를 기록. 이러한 높은 보상 정확도는, 테스트 데이터 상에서 TTRL이 효과적인 자기 개선(self-improvement)을 수행할 수 있는 신뢰할 만한 기반이 됨.
4.3 Q3: When Might TTRL Fail?
- 알고리즘적 관점에서 볼 때, TTRL은 기존의 강화학습(RL) 알고리즘과 근본적으로 다른 방식은 아니며, 따라서 기존 RL이 가지는 몇 가지 특성을 함께 지님. 예를 들어, 데이터 난이도에 대한 민감성, 사전 지식(prior)에 대한 강한 의존성, 특정 조건에서의 붕괴(collapse) 위험 등이 있음.
- 구현 관점에서는, TTRL이 다수결 투표로 라벨을 추정하고, 드물고 사전 학습에 사용되지 않은 테스트 데이터만을 대상으로 작동한다는 제약으로 인해, 이러한 문제점들이 더욱 심화될 수 있음. 이로 인해 TTRL은 특정 시나리오에서 실패할 가능성이 있음.
목표 과제에 대한 사전 지식 부족
- 강화학습에서는 사전 지식이 매우 중요한 역할을 하며, 이는 TTRL의 성공 여부를 결정짓는 핵심 요소 중 하나로 작용함. 이는 일반적으로 테스트 데이터가 더 높은 난이도를 가지며 새로운 특성을 포함하고 있지만, TTRL에는 데이터 필터링이나 커리큘럼 러닝을 지원하는 메커니즘이 없기 때문.
- 따라서 같은 백본 모델이라 하더라도, 데이터 복잡성을 감당할 만큼의 사전 지식이 부족한 경우 TTRL은 실패함. 실제로 Qwen2.5-Math-1.5B와 LLaMA-3.1-8B-Instruct 모델이 AIME 2024에서 성능 향상을 보이지 못한 이유는 여기에 있다고 가정할 수 있음. 반면, 동일한 백본으로 더 간단한 벤치마크에서는 TTRL이 성능 향상을 보였기 때문.
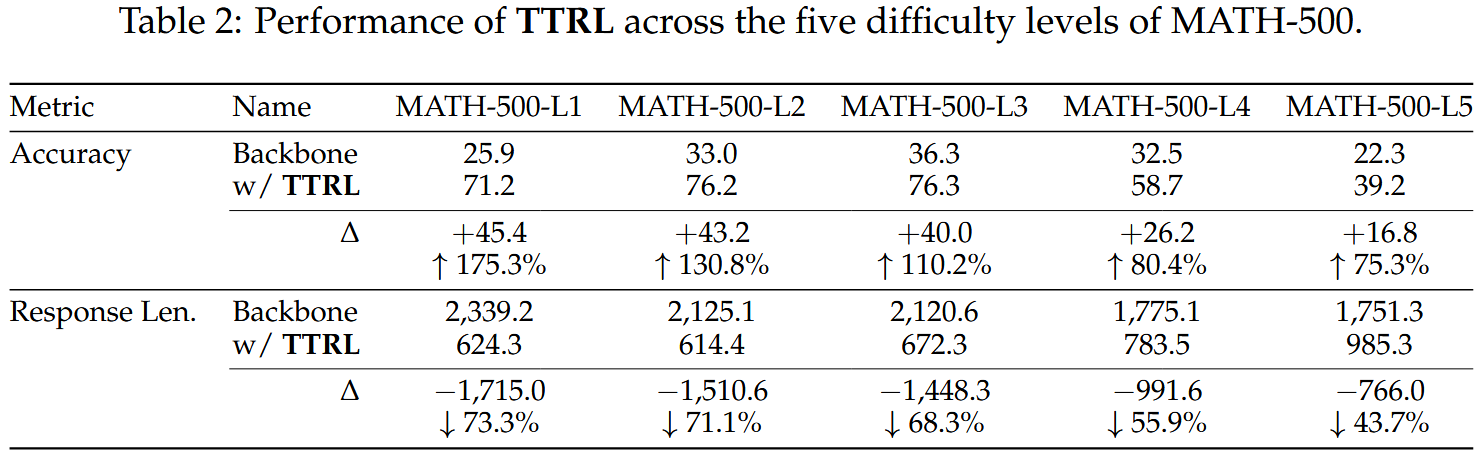
- 이 가설을 검증하기 위해, 우리는 MATH-500에 대한 ablation study을 수행함. MATH-500을 주석된 난이도 수준에 따라 1에서 5까지 다섯 개의 서브셋으로 나눈 뒤, 각각에 대해 Qwen2.5-Math-1.5B를 사용하여 TTRL을 독립적으로 적용함. 그 결과를 백본 모델의 성능과 비교한 결과, 문제의 난이도가 높아질수록 성능 향상률과 응답 길이 감소율 모두 하락하는 경향을 보임 (Table 2).
- 이는, 백본 모델이 가진 사전 지식만으로는 난도가 높은 질문에 대한 학습을 뒷받침하기에 충분하지 않다는 것을 시사함.
부적절한 RL 하이퍼파라미터 설정
- 하이퍼파라미터 설정은 RL 훈련에서 매우 중요한 변수이며, 프로젝트마다 다르게 적용되며 학습 실패의 원인이 되기도 함.
TTRL에서는 보상 추정의 노이즈와 테스트 데이터의 특성 때문에 하이퍼파라미터의 영향력이 더 커지는 경향이 있음. - Fig. 10은 AIME 2024에서 실패한 여러 실험 설정을 비교한 결과. 두 경우 모두 훈련 도중 엔트로피가 지속적으로 높게 유지되며 감소하지 않았고, 이는 기존 연구에서도 보고된 실패 패턴과 일치함.

- 사전 실험을 통해, TTRL의 학습 안정성과 성공에 결정적인 영향을 미치는 두 가지 주요 하이퍼파라미터를 확인함:
- Temperature:
- Temperature를 0.6 대신 1.0으로 설정하면, 모델의 출력 엔트로피가 증가하여 더 넓은 탐색을 유도하게 됨. 이는 모델이 자신의 사전 지식을 보다 효과적으로 활용하여 자기 개선을 할 수 있게 하며, 특히 난이도 높은 벤치마크에 대응할 때 매우 중요.
- Episodes:
- 데이터셋마다 크기와 난이도가 크게 달라지기 때문에, 더 작고 난이도 높은 데이터셋일수록 더 많은 에피소드를 통해 충분한 탐색이 필요함.
6 Conclusions
- 본 논문에서는 정답 label 없이 테스트 데이터에서 RL을 통해 대형 언어 모델을 학습시키는 새로운 프레임워크인 Test-Time Reinforcement Learning(TTRL)을 제안함.
- TTRL의 핵심 요소는 모델 예측 간의 합의를 바탕으로 규칙 기반 보상을 생성하는 다수결 보상 함수임. 실험 결과, TTRL은 다양한 모델과 과제에서 일관된 성능 향상을 보여주며 높은 가능성을 입증함. 우리는 TTRL을 자기 라벨 보상을 활용한 강화학습을 향한 초기 단계로 보고 있으며, 이는 지속적인 경험의 흐름으로부터 학습하는 중요한 방향성을 제시함.
7 Limitations and Future Works
- 본 연구는 selflabeled reward을 활용한 TTRL에 대한 초기 탐색에 해당. 실험 결과는 유망하지만, 여전히 추가적인 검토가 필요한 여러 측면이 존재. 특히, 사전 지식과 하이퍼파라미터 설정이 강화학습의 동적 특성에 중요한 영향을 미치기 때문에, 이에 대한 보다 심층적인 분석이 필요. 본 논문의 향후 개정판에서는 이에 대한 종합적인 논의와 ablation study을 제공할 예정임.
- 이번 연구 결과를 바탕으로, 우리는 다음과 같은 여러 향후 연구 방향을 제시
- 이론적 분석: TTRL의 수렴 특성에 대한 공식적인 분석을 수행하며, 특히 4.1절에서 제시된 두 가지 상한선에 수렴할 수 있는 능력을 중심으로 검토할 예정.
- 스트리밍 데이터 기반 온라인 학습: 지속적으로 도착하는 데이터와 상호작용하며 실시간으로 적응하는 학습 시나리오로 TTRL을 확장하는 방안을 모색.
- 대규모 자기지도 강화학습: 인위적인 레이블 없이, 대규모 데이터셋과 모델에 대해 TTRL을 확장하여 self-supervised RL 환경에서의 가능성을 탐구.
- 에이전트 기반 과제 및 과학적 발견: TTRL을 보다 복잡하고 열린 형태의 과제, 예를 들어 에이전트 기반 작업이나 다단계 과학적 추론 등으로 적용하는 방향을 고려.
'AI 공부 > 논문 리뷰' 카테고리의 다른 글
| [논문 리뷰] Qwen2.5-Omni Technical Report (0) | 2025.05.10 |
|---|---|
| [논문 리뷰] xVerify: Efficient Answer Verifier for Reasoning Model Evaluations (0) | 2025.04.27 |
| [논문 리뷰] ReTool: Reinforcement Learning for Strategic Tool Use in LLMs (2) | 2025.04.20 |